SQL Server, DECIMAL and FLOAT data types. Are you ready to deep dive into the secrets of SQL Server?
 Hi guys!
Hi guys!Welcome back and thanks for the many visits to this blog! I won't hide the fact that I'd like to reach 5,000 visits by the end of the year!
Who knows?
Today we talk about decimal and float data type in SQL Server
Are you Ready to a deep dive into the secrets of SQL Server?
Prima di tutto, ben ritrovati e grazie per le molte visite a questo blog!
Non nascondo il fatto che mi piacerebbe raggiungere le 5.000 visite entro la fine dell'anno!
Chissà?
Oggi parleremo dei tipi di dati decimal e float.
Siete pronti per immergervi nei segreti di SQL Server?
I tipi di dato decimal e float
 Iniziamo oggi a parlare di tipi di dato. Lo facciamo raccontando del tipo di dato Decimal per poi passare al tipo di dati float.
Iniziamo oggi a parlare di tipi di dato. Lo facciamo raccontando del tipo di dato Decimal per poi passare al tipo di dati float.
Un concetto importante: Mentre il tipo di dato Decimal (o NUMERIC: sono sinonimi) è un tipo di dato che si dice non approssimato, il float è invece un tipo di dato approssimato. Vedremo sotto cosa significa.
Il tipo di dati DECIMAL.
Partiamo dalla sua dichiarazione.
Un tipo di dati decimal è definito così:
DECLARE @value1 DECIMAL(18,5)
Vediamo subito che questo tipo di dato prevede la possibilità di specificare nella sua definizione due valori.
Il primo valore è detto precisione, l’altro è detto scala.
Per default, se la precisione se non specificata è pari a 18, mentre i valori accettati sono da 1 a 38
I valori accettati per la scala sono da 1 fino al valore della precisione.
E' la precisione che si vuole adoperare che determina l’occupazione di spazio.
Come possiamo vedere dalla tabella sotto, se la precisione è minore o uguale a 9 il nostro numero decimal sarà memorizzato in 5 bytes. Precisioni maggiori richiedono ovviamente spazio di memorizzazione maggiore.
Precisions
|
Storage bytes
|
1 - 9
|
5
|
10-19
|
9
|
20-28
|
13
|
29-38
|
17
|
A Deep Dive into decimal
So che siete curiosi di vedere come viene memorizzato sul database?
Per memorizzarlo sul database in formato DECIMAL mi vado a creare una tabella con un campo di tipo DECIMAL che ha precisione 18 e scala 5.
Così:
CREATE TABLE dbo.Numbers
(
val DECIMAL(18, 5)
)
Poi inserisco nella tabella in nostro numero tramite il commando SQL:
Insert into Numbers(c1) values (100.12345)
Ora siamo pronti per indagare!
Vediamo come viene memorizzato questo dato dallo storage engine.
Per prima cosa cerchiamo in quale pagina di memoria si trova la nostra tabella Numbers scrivendo il comando T-SQL:
Per prima cosa cerchiamo in quale pagina di memoria si trova la nostra tabella Numbers scrivendo il comando T-SQL:
DBCC IND('TEST',Numbers,-1)
Se lo eseguiamo ci restituisce che la nostra tabella si trova nella pagina 8376
Adesso andiamo a vedere cosa contiene questa pagina scrivendo i comandi T-SQL:
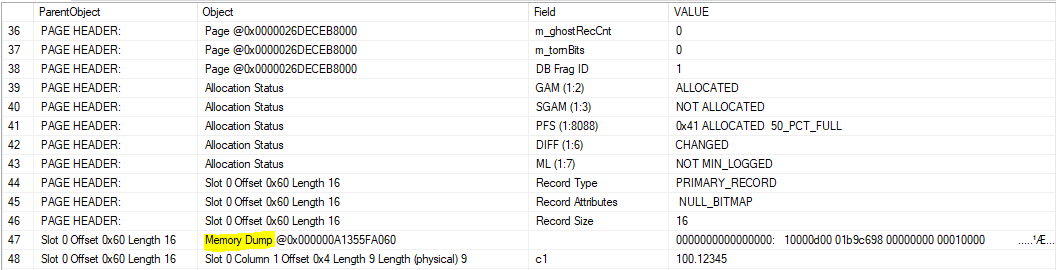
La riga che occorre guardare è quella evidenziata in giallo con la scritta Memory Dump.
Possiamo leggere questi 16 bytes.
DBCC TRACEON(3604)
DBCC PAGE('TEST',1,8376,3) WITH TABLERESULTS
La riga che occorre guardare è quella evidenziata in giallo con la scritta Memory Dump.
Possiamo leggere questi 16 bytes.
0000000000000000: 10000d00 01b9c698 00000000 00010000 .....¹Æ.........
Sappiamo che il nostro valore in Decimal occupa una lunghezza di 9 byte.
0000000000000000: 10000d00 01b9c698 00000000 00010000 .....¹Æ.........
Se leggiamo ora da destra a sinistra la parte evidenziata della stringa esadecimale abbiamo questo valore:
000000000098c6b9
000000000098c6b9
10012345
Che, al netto della virgola dopo i primi 3 caratteri è il nostro valore:
100.12345
Ed il numero 01 cos'è?
L'ultimo byte è il segno: 01 significa che il numero è maggiore di 0.
Viceversa che avessimo trovato un valore di 00 il nostro numero sarebbe stato negativo.
Tutto questo per ribadire un concetto importante: quando rappresentiamo un numero in formato DECIMAL memorizziamo effettivamente tutti i decimali.
Per questo motivo si parla di numero non approssimato.
Questo tipo di dato è infatti quello più indicato per memorizzare ad esempio di importi.
Il tipo di dato float
Vediamo ora come funziona il tipo di dato float.
Due considerazione fondamentali:
- Un float è un numero approssimato.
- Non tutti i numeri espressi in float posso essere rappresentati.
Come direte voi?
Immaginate di voler memorizzare il valore 0.1 in float bhe in float una rappresentazione esatta non esiste.
Vediamo ora perchè analizzando come viene memorizzato il nostro numero 100.12345 nel formato float.
Per fare questo creiamo una tabella con un campo float ed inseriamo un valore.
CREATE TABLE dbo.Numbers3
(
val float
)
Insert into Numbers3(val) values (100.12345)
Adesso vediamo come è rappresentato internamente il nostro numero.
Come abbiamo già fatto per i decimal eseguiamo i seguenti comandi
DBCC IND('test_temp_table',Numbers3,-1)
DBCC TRACEON(3604)
DBCC PAGE('test_temp_table',1,1152,3) WITH TABLERESULTS
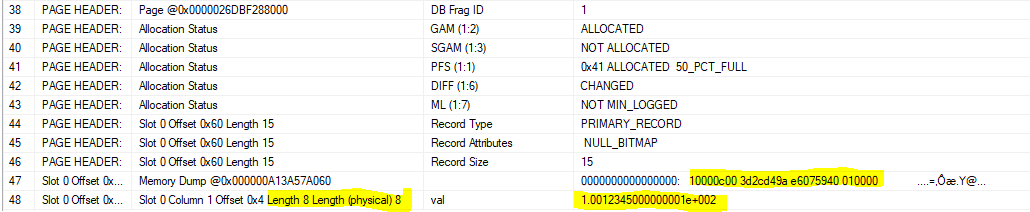
Intanto vediamo che il nostro valore float viene memorizzato in uno spazio di 8 byte.

Abbiamo il valore 3d2cd49ae6075940.
Questa volta decodificarlo è un po più complesso.
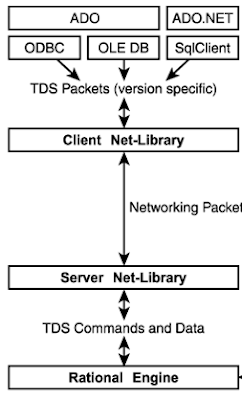
Secondo lo schema riportato sotto, abbiamo da sinistra a destra:
1) Un bit per il segno
2) Un esponente di 11 bit
3) 52 bit di mantissa
Invertiamo il valore leggendolo da destra a sinistra ed otteniamo:
405970e69ad42c3d
Convertiamo quindi il nostro valore in formato binario:
0100000001011001011100001110011010011010110101000010110000111101
dove:
Il primo 0 a sinistra è il segno
L'esponente è pari a 10000000101
La mantissa è 1001011100001110011010011010110101000010110000111101
Prendiamo l'esponente e convertiamolo in decimale
10000000101 = 1029
Sottraiamo da 1029 il valore 1023 ed otteniamo 6
il primo valore sarà 2^6 = 64
Prendiamo ora la mantissa, aggiungiamo un 1davanti, e convertiamola in decimale ed otteniamo:
7397405160123453
Ora dividiamo la mantissa per 2^52 e otteniamo questo valore:
1.6425539062500000841
Se ora moltiplichiamo questo valore per 64 otteniamo questo numero:
105.1234500000000053824
Importante, vi ricordate quando dicevo ad inizio paragrafo che il tipo di dato float è approssimato? E proprio vero!
Ho scritto nel database il numero 105.12345 ma ho memorizzato un numero leggermente diverso che è 105.1234500000000053824
Per questo motivo il tipo di dati float non è indicato per memorizzare valori in cui la precisione assoluta è importante!
Spero di essere riuscito a descrivere chiaramente il funzionamento dei due tipi di dato decimal e float.
Se vi è piaciuto l'articolo allora rimanete in attesa del prossimo artico!
Alla prossima!
Float and Decimal Data Types
 We begin today to talk about data types. We do this by telling about the Decimal data type and then switching to the float data type.
We begin today to talk about data types. We do this by telling about the Decimal data type and then switching to the float data type.
An important concept: While the Decimal data type (or NUMERIC: they are synonyms) is a type of data that is said to be not approximate, the float is instead an approximate data type.
We will see below what it means.
The DECIMAL data type.
Let's start with your statement.
A decimal data type is defined like this:
DECLARE @value1 DECIMAL(18,5)
We see immediately that this type of data provides the possibility to specify two values in its definition.The first value is called precision, the other is called scale.
By default, if the precision if not specified is equal to 18, while the accepted values are from 1 to 38
The accepted values for the scale are from 1 up to the precision value.
It is the precision we want to use that determines the occupation of space.
As we can see from the table below, if the precision is less than or equal to 9 our decimal number will be stored in 5 bytes.
Greater precision obviously requires more storage space.
Precisions
|
Storage bytes
|
1 - 9
|
5
|
10-19
|
9
|
20-28
|
13
|
29-38
|
17
|
A Deep Dive into decimal!
Are you curious to see how a decimal data type is stored inside the database? yes?
So let's take a decimal number, suppose the number 100.12345.
To store our number on the database in DECIMAL format I'm going to create a table with a DECIMAL type field that has precision 18 and scale 5.
So:
CREATE TABLE dbo.Numbers
(
val DECIMAL(18, 5)
)
Then I insert in the table the number through the SQL command:
Insert into Numbers(c1) values (100.12345)
Now we are ready to investigate!
Let's see how this data is stored by the storage engine.
First let's look in which page of memory our Numbers is located by writing the command T-SQL:
DBCC IND('TEST',Numbers,-1)
If we execute it it returns us that our table is found on page 8376
We can read these 16 bytes.
0000000000000000: 10000d00 01b9c698 00000000 00010000 .....¹Æ.........
We know that our value in Decimal takes up a length of 9 bytes.
0000000000000000: 10000d00 01b9c698 00000000 00010000 .....¹Æ.........
If we now read the highlighted part of the hexadecimal string from right to left we have this value:
000000000098c6b9
If we convert it to decimal we will have:
10012345
That, at net of the comma after the first 3 characters is our value:
100.12345
And the number 01 what is it?
The last byte is the sign: 01 means that the number is greater than 0.
Conversely, if we had found a value of 00, our number would have been negative.
All this to reiterate an important concept:
When we represent a number in DECIMAL format we actually store all the decimals.
For this reason we speak of a non approximate number.
This type of data is in fact the most suitable for storing, for example, amounts.
Two fundamental considerations:
The float data type
Now let's see how the float data typeworks.Two fundamental considerations:
- A float is an approximate number.
- Not all numbers expressed in float can be rapresented.
Imagine you want to store the value 0.1 in float
Well in float an exact representation simply doesn't exist.
Now let's see why analyzing how our number 100.12345 is stored in the float format
To do this we create a table with a float field and insert a value.
Now let's see how our number is represented internally. As we have already done for the decimal we execute the following commandsCREATE TABLE dbo.Numbers3 ( val float ) Insert into Numbers3(val) values (100.12345)
DBCC TRACEON(3604)
DBCC PAGE('test_temp_table',1,1152,3) WITH TABLERESULTS

Meanwhile, we see that our float value is stored in a space of 8 bytes.
We have tha value 3d2cd49ae6075940.
This time decoding it is a little more complex.
This time decoding it is a little more complex.
According to the diagram below, we have from left to right:
1) A bit for the sign
2) An exponent of 11 bits
We reverse the value reading it from right to left and we get:
405970e69ad42c3d
We then convert our value into binary format:
0100000001011001011100001110011010011010110101000010110000111101
where:
- The first 0 to the left is the sign
- The exponenent is 10000000101
- The mantissa is 1001011100001110011010011010110101000010110000111101
Let's take the exponent and convert it to decimal
10000000101 = 1029
We subtract from 1029 the value 1023 and we get 6
The first value will be 2^6 = 64
Let's take the mantissa, add an one before, and convert it to decimal and we get:
7397405160123453
Now divide mantissa by 2^52 and we get this value:
1.6425539062500000841
If we now multiply this value by 64 we get this number:
105.1234500000000053824
Important:
Do you remember when I said at the beginning of the paragraph that the type of data float is approximate? It's really true!
Because I wrote the number 105.12345 in the database but I memorized a slightly different number which is 105.1234500000000053824
For this reason the float data type is not suitable for storing values where absolute precision is important!
I hope I was able to clearly describe the operation of the two decimal and float data types.
If you liked the article, then look forward to the next article!
See you soon!
Next post: SQL Server, Math and ApplicationsSee you soon!
Luca Biondi @ SQLServerPerformance blog!
Previous post: SQL Server trigger optimization part 1











Molto interessante. Grazie
ReplyDeletethanks for providing wonderful information on SQL Server, DECIMAL, keep posting Software Testing Classes in Pune
ReplyDelete